近日,一場關於大型推理模型能力邊界的學術爭論在 AI 研究領域掀起波瀾。繼蘋果公司發表論文質疑 DeepSeek-R1 等大型推理模型的根本能力後,社區內許多研究者紛紛對其提出質疑,認爲蘋果的結論更像是出於其在 AI 競賽中暫時的落後而“喫不到葡萄說葡萄酸”。與此同時,針對研究內容本身的嚴謹性質疑也紛至沓來,甚至連 AI 模型本身也親自下場,參與到了這場激烈的辯論之中。
來自 Open Philanthropy 的研究員 A. Lawsen 利用 Claude Opus 爲第一作者發表了一篇針鋒相對的反駁論文,題爲《思考幻覺的幻覺:對 Shojaee 等人 (2025) 的評論》(The Illusion of the Illusion of Thinking: A Comment on Shojaee et al. (2025))。

圖丨相關論文(來源:arXiv)
在我們此前的報道中已經詳細介紹過,蘋果公司的研究團隊通過讓模型解答各種謎題,發現 DeepSeek-R1、o3-mini 和
Claude-3.7-Sonnet-Thinking 等前沿大型推理模型在超過某一複雜度閾值之後,準確率會出現全面崩潰。蘋果研究團隊認爲,這表明這些模型並未真正發展出可泛化的推理能力,而只是在進行某種形式的模式匹配。例如,模型可以在漢諾塔中完成多達 100 個正確的動作,但在邏輯推理遊戲渡河謎題中卻無法給出超過 5 步的正確操作。
然而,這篇反駁論文以及其他相關質疑都指向了一個根本性問題:蘋果團隊的發現主要反映了實驗設計的幾個侷限性,而非模型的根本性推理失敗。第一個核心問題是“物理令牌限制驅動了表象上的崩潰”。
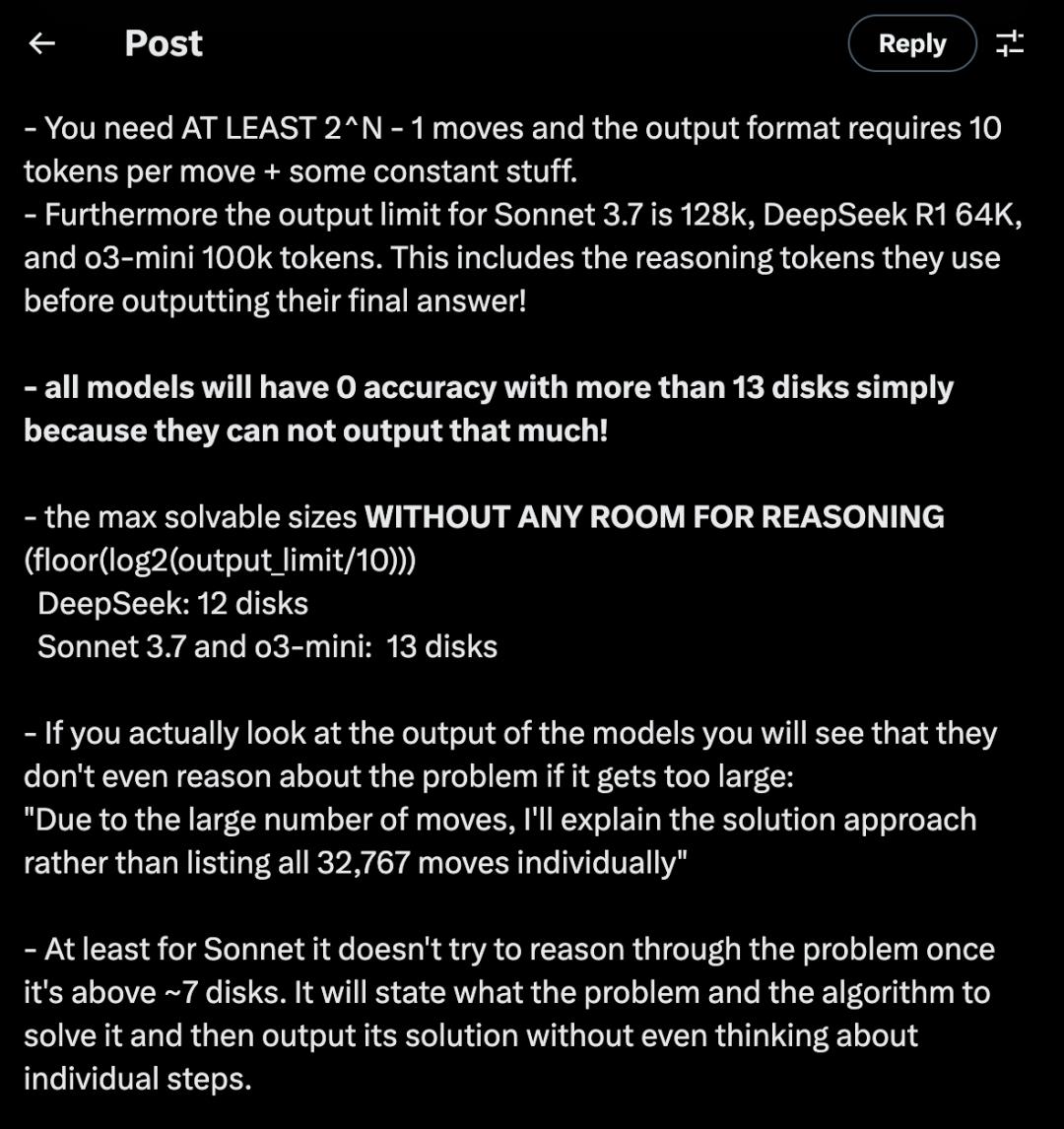
Claude 的研究發現,在蘋果報告的失敗點上,漢諾塔實驗系統性地超出了模型的輸出 token 限制。論文引用了 X 用戶 @scaling01 的復現實驗,他捕獲到模型輸出明確表示:“模式繼續,但爲了避免過長,我將在這裏停止”。
@scaling01 指出,漢諾塔至少需要 2^N-1 次移動,而蘋果使用的輸出格式每次移動需要 10 個 token 加上一些常量。更關鍵的是,不同模型的輸出限制差異很大:Sonnet 3.7 爲 128k token,DeepSeek R1 爲 64k token,o3-mini 爲 100k token,這些限制還包括模型在輸出最終答案前使用的推理 token。
圖丨相關推文(來源:X)
這意味着所有模型在超過 13 個盤子時準確率都會變爲零,純粹是因爲它們無法輸出那麼多內容。@scaling01 計算出,在沒有任何推理空間的情況下,最大可解決大小爲:DeepSeek 12 個盤子,Sonnet 3.7 和 o3-mini 13 個盤子。當實際觀察模型輸出時會發現,如果問題變得太大,模型甚至不會對問題進行推理,而是直接表示“由於移動次數龐大,我將解釋解決方法而不是逐一列出所有 32,767 次移動”。
Claude 論文量化了這種關係:蘋果的評估格式要求在每個步驟輸出完整的移動序列,導致二次 token 增長。如果每個序列中的移動大約需要 5 個 token,那麼總 token 需求 T(N) ≈ 5(2^N - 1)^2 + C。給定分配的 token 預算,最大可解決大小完全可以通過數學公式預測,而報告的“崩潰”正好與這些物理約束一致。
@scaling01 還發現了一個有趣的現象:對於 Sonnet 來說,一旦超過大約 7 個盤子,它就不會嘗試推理問題。它會說明問題是什麼以及解決它的算法,然後輸出解決方案而不考慮個別步驟。這種行爲模式進一步支持了 Claude 論文的觀點,即模型理解問題和算法,但受到輸出格式的限制。
更爲嚴重的問題出現在河流渡河實驗中。Claude 論文指出,蘋果團隊測試了 N≥6 個行爲者使用船隻容量 b=3 的實例,但這是一個早已確立的數學結果:傳教士-食人族謎題及其變體對於 N>5 且 b=3 的情況根本沒有解決方案。通過自動將這些不可能的實例評爲失敗,研究團隊無意中展示了純程序化評估的危險——模型得到零分不是因爲推理失敗,而是因爲正確識別了不可解決的問題。
@scaling01 從另一個角度分析了複雜性度量的問題。他指出,蘋果研究使用最優路徑長度作爲問題複雜性的代理指標是根本錯誤的,因爲它沒有告訴我們找到任何解決方案有多困難,只是告訴我們解決方案的長度。即使漢諾塔的搜索空間巨大,你實際上不必執行任何搜索或回溯,因爲只有一個簡單的規則要應用(大型語言模型知道),因此只有一條可能的路徑。
爲了驗證這一觀點,@scaling01 讓 o3 和 Gemini 2.5 Pro 搜索遊戲複雜性的其他更合適的指標,結果一致地將遊戲難度排名爲:河流渡河>>積木世界>跳棋跳躍>漢諾塔。這一排名也與蘋果研究的圖表中顯示的內容完全一致,這意味着蘋果團隊的“模型可能在較低組合深度的謎題上遇到困難,同時在較高組合深度的不同謎題上取得成功”。這一發現並不令人意外,而是完全可以預期的。
除了上述問題,還有研究者質疑了使用漢諾塔這類知名謎題測試推理能力的合理性。他指出,如果擔心數學和編程基準存在污染問題,爲什麼要選擇解決方案已知存在於訓練數據中的著名謎題?漢諾塔算法在模型訓練數據中反覆出現,給模型提供算法當然不會有太大幫助——模型已經知道算法是什麼。此外,推理模型經過了數學和編程的專門訓練,而不是謎題訓練。有用戶指出這就像說“語言模型在寫彼特拉克十四行詩方面沒有比 GPT-3.5 好多少,所以我認爲沒有取得真正的進步”。
圖丨相關博文(來源:sean goedecke)
對於蘋果研究聲稱的“複雜度閾值”意味着模型無法推理的觀點,許多網友提出了一個靈魂拷問:“多少人類能夠坐下來正確計算出一千步漢諾塔?”答案是極少數。但這是否意味着那些做不到或不願做的人就不具備推理能力?當然不是。他們只是缺乏執行上千次枯燥迭代的耐心和細緻。正如一位 Reddit 用戶所說:“人類能推理,不代表人類有能力寫下幾千步的漢諾塔。反之,寫不下幾千步也不代表它不能推理。”
當然,這種將模型行爲“擬人化”的解讀也並非沒有爭議。另一派評論者認爲,將模型的行爲描述爲“不願意”或“尋找捷徑”是一種過度解讀。他們指出,關鍵在於模型在面對更復雜的 8、9、10 盤問題時,甚至連通用的遞歸算法都沒能成功導出,這足以說明其推理能力在根本上是脆弱的,僅僅是在模擬簡單情況下的推理模式。
爲了進一步證明問題出在評估方法而非模型能力,Claude 的研究進行了一個關鍵實驗。他們對相同模型進行了漢諾塔 N=15 的測試,但使用了不同的表示方法:要求模型輸出一個調用時打印解決方案的 Lua 函數,而不是詳盡列舉所有移動步驟。結果顯示,在測試的模型中準確率很高,在不到 5,000 個 token 內完成。生成的解決方案正確實現了遞歸算法,展示了當擺脫詳盡枚舉要求時模型完整的推理能力。
論文總結道,蘋果的研究結果實際上揭示了一些有價值的工程性見解:模型無法輸出超過其上下文限制的令牌、程序化評估可能會錯過模型的能力和謎題本身的可解性,以及解決方案的長度並不能很好地預測問題的難度。但是,這些都不能支持其關於“模型存在根本性推理侷限”的核心主張。
“問題的關鍵可能不在於大型推理模型能否推理,而在於我們的評估體系是否能夠將推理能力與‘打字’能力區分開來。”
參考資料:
1.https://arxiv.org/pdf/2506.09250v1
2.https://www.seangoedecke.com/illusion-of-thinking/
3.https://x.com/scaling01/status/1931783050511126954
運營/排版:何晨龍