近日,美國卡內基梅隆大學助理教授陳貝迪和團隊提出了“動力學擴展定律”(Kinetics Scaling Law)。在該定律的指導之下,當在英偉達 B200 上實現相同精度時,資源需求最高可降低至原來的三分之一。

圖 | 陳貝迪(來源:http://publish.illinois.edu/rising-stars/beidi-chen/)
同樣是在該定律的指導之下,在 AIME 和 LiveCodeBench 上,稀疏注意力在低成本模式下將問題解決率提高了 60%,在高成本模式下提高了 5% 以上。
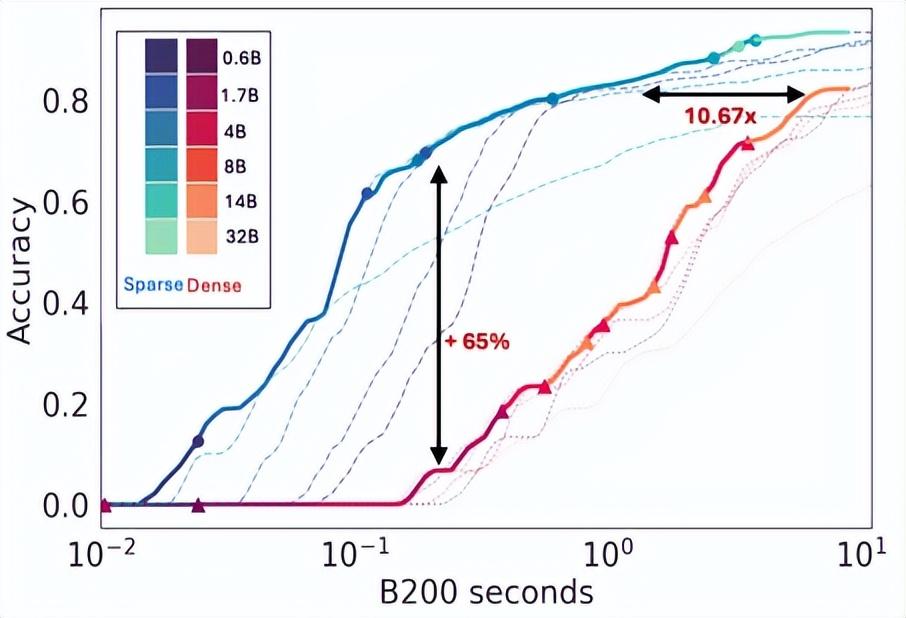
(來源:arXiv)
動力學擴展定律的核心觀點是:在測試時擴展(TTS,Test-time scaling)任務中,影響性能的主要因素不是參數數量,而是注意力機制的計算成本。
本次研究團隊證明,稀疏注意力從根本上重塑了擴展格局,使得生成內容的長度更長、精度更高。其在論文中表示,稀疏動力學可能預示着一種新範式,這種新範式使得即便在預訓練進入平臺期後仍能推動持續進步。
研究中,他們還強調了將模型架構、測試時推理技術與硬件基礎設施進行協同設計的必要性,並認爲這是推動下一波可擴展大模型部署的關鍵步驟。雖然本次分析主要集中在英偉達 GPU 上,但“擴展內存帶寬比擴展浮點運算(FLOP,floating-point operation)能力更具挑戰性且成本更高”這一基本原理廣泛適用於各類硬件平臺,因此本次成果具有一定的普適性。

降低每個 token 的計算成本,支持更長的文本生成和更多的並行樣本處理
研究團隊表示,他們從實際效率的角度重新思考了測試時擴展定律,發現較小模型的有效性實際上被嚴重高估了。具體來說,此前人們基於計算最優性的研究工作,其實忽略了推理時策略所引入的關鍵內存訪問瓶頸問題。
而在本次研究之中,他們全面分析涵蓋了從 0.6B 到 32B 參數的模型,藉此揭示了動力學擴展定律,該定律通過同時納入計算成本和內存訪問成本,能夠更好地指導資源分配。
動力學擴展定律表明,在參數超過某個閾值的模型上使用測試時計算,比在較小模型上使用更爲有效。一個關鍵原因是在測試時擴展中,注意力纔是主要的成本因素(而非參數數量)。
受此啓發,研究團隊提出了以稀疏注意力爲中心的新擴展範式,該範式可以降低每個 token 的計算成本,從而能在相同的資源預算下,支持更長的文本生成和更多的並行樣本處理。
研究團隊發現,稀疏注意力模型始終優於密集註意力模型。這說明隨着計算投入的增加,稀疏注意力是必不可少的,而且會越來越重要,只有這樣才能實現測試時擴展的全部潛力。而與訓練不同的是,準確性並未隨着計算的增加而飽和,而是會通過增加生成量不斷得到提高。
那麼,研究團隊開展本次課題的原因是什麼?這要從測試時擴展(TTS,Test-time scaling)說起。眼下,測試時擴展策略已經成爲增強大模型推理能力的一種重要手段,特別是在智能體與複雜環境交互的場景中,例如編寫代碼、瀏覽網頁等場景中。
然而,這些能力會帶來顯著的推理時成本,因此理解這一新範式下的性能擴展規律至關重要。現有的擴展定律研究主要關注浮點運算(FLOP,floating-point operation),但卻忽略了內存訪問成本。而內存訪問成本往往是決定實際延遲的關鍵因素,因此上述做法可能會導致部署決策不夠優化。
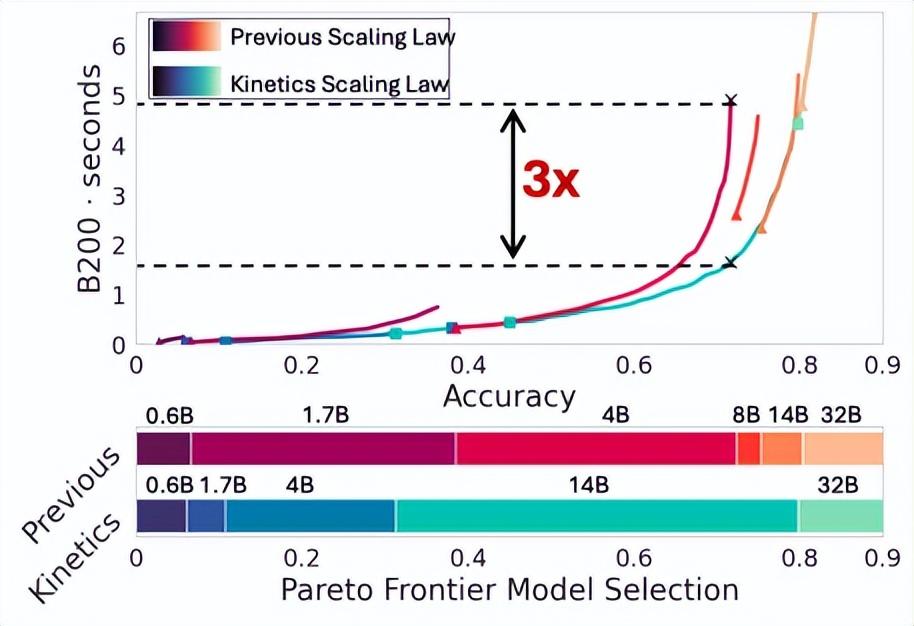
(來源:arXiv)
如前所述,在本次研究之中他們展示了測試時擴展的動力學擴展定律,該定律源自於一個明確納入內存訪問成本的成本模型,它揭示了關於測試時計算資源分配的帕累托最優策略的截然不同的結論。
具體而言,研究團隊發現:首先,先前的標度律始終高估了通過推理時策略增強的小模型的有效性;其次,計算資源最好先用於將模型規模增大到一個關鍵閾值,然後再投入測試時策略。
研究中,他們針對一系列最先進的推理模型所進行的屋頂線分析表明:之所以出現最優測試時計算策略的轉變,是因爲測試時策略不成比例地增加了注意力成本,而非增加了參數成本。
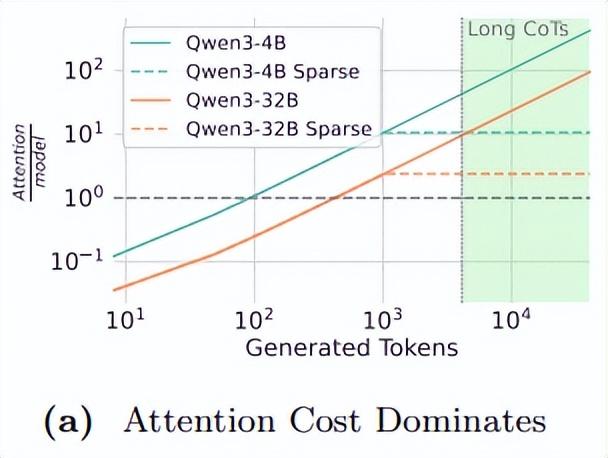
(來源:arXiv)
研究團隊的等成本分析表明,注意力機制隨生成長度呈二次方增長的特性,加上鍵值內存相對於模型參數的失衡擴展趨勢,共同使得人們更加傾向於擴大模型規模、而非增加生成長度。這種失衡現象在混合專家架構中被進一步加劇,正因此這種架構雖然能夠降低激活參數量,但卻未能緩解注意力計算的高開銷現狀。
基於上述分析,研究團隊引入了本次新的擴展範式,該範式以稀疏注意力爲中心,從根本上重塑了擴展規律,顯著提高了測試時擴展的可擴展性。
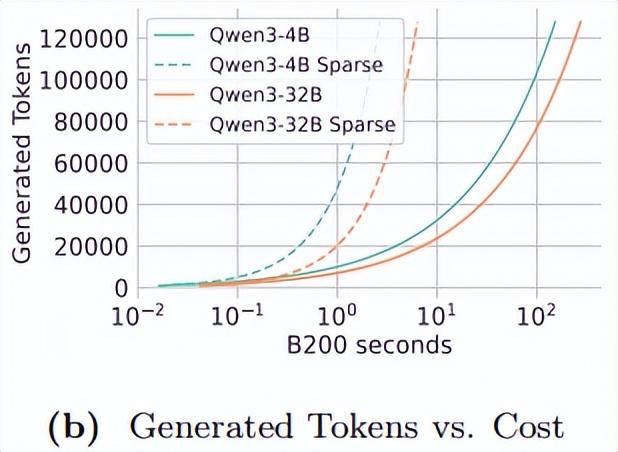
(來源:arXiv)
根據研究團隊的稀疏動力學擴展定律,最好將計算資源分配給測試時策略,而非用於降低稀疏性。隨着在測試階段投入更多計算資源,高稀疏性對於充分利用這些策略的優勢變得愈發關鍵。
儘管稀疏性傳統上要麼用於小模型的正則化,要麼用於在參數過多的網絡中減少計算量,但本次研究引入了一個根本不同的視角——稀疏性能夠成爲實現高效可擴展測試時計算的核心使能技術。與此同時,本次研究強調了在建立可擴展性定律的實際認知過程中,必須同時考量硬件因素與模型架構的重要性。

讓 Qwen3-0.6B 模型實現 23.6∼33.3 倍的吞吐量增長
在實驗設置和實驗任務上,研究團隊聚焦於以下三個具有一定挑戰性的推理基準:涵蓋代數、組合數學和幾何的 AIME24 和 AIME25,以及包含近期編程競賽中的複雜編程問題的 LiveCodeBench。在模型選擇上,研究團隊評估了 Qwen3 和 DeepSeek-R1-DistilledQwen 系列不同模型的性能。
爲了消除測試時策略的具體實現所引入的混雜效應,研究團隊採用了兩種具有代表性但簡單的方法:長 CoT 和 Best-of-N。長 CoT 是一種在先進推理模型中被廣泛使用的方法,Best-of-N 則通過可驗證問題的解決率進行效果評估,並藉助測試時間擴展給出理論性能上限。
在硬件上,研究團隊使用了英偉達 B200。實驗中,他們在每個節點 8 個 GPU 上,通過批量大小和上下文長度分別爲(4096,16384)和(2048,32768)的設置,展示了塊 top-k 注意力在不同模型規模下的優勢。
同時,他們假設具有相似上下文長度和生成長度的任務的工作負載是統一的。如下圖所示,塊 top-k 注意力能夠大大提高推理吞吐量,特別是對於較小的模型來說。例如,Qwen3-0.6B 模型實現了 23.6∼33.3 倍的吞吐量增長。
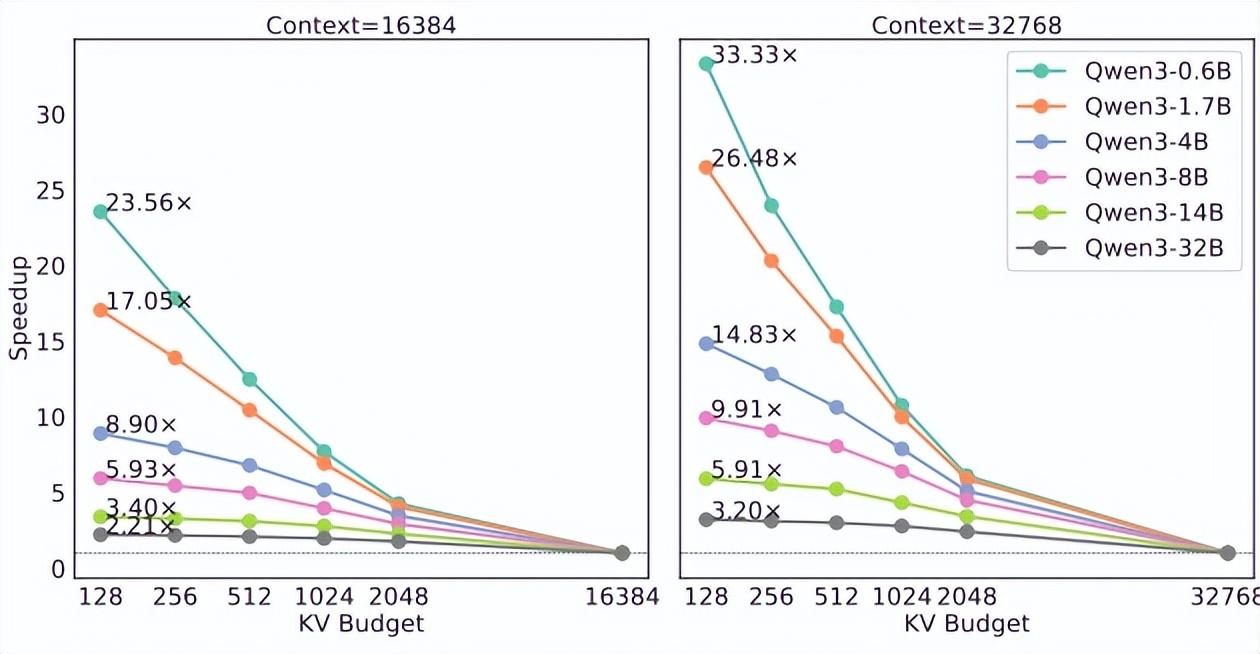
(來源:arXiv)
這一性能提升反映出:隨着上下文長度的增加,稠密注意力機制的效率會逐漸下降,而較小模型受到的影響尤爲顯著。吞吐量的顯著提升凸顯了這樣一種潛力:當與推理系統和測試時策略進行適當的協同設計時,任務級吞吐量也能獲得相應的提升。
除了 top-k 注意力機制之外,目前他們僅探討了一種簡單的變體(即塊 top-k 注意力),儘管如此已能展現出強大的可擴展性。眼下,已經存在更先進的稀疏注意力算法,這些算法具備將測試時擴展效率的邊界推向更高水平的潛力。
另一方面,測試時擴展算法旨在自適應地將計算資源分配給任務甚至是分配給 token。將它們擴展到稀疏注意力中的新資源分配問題,對於達到稀疏動力學的極限至關重要。例如,由於生成長度與稀疏注意力下的最佳試驗次數密切相關,因此可以將其用作調整試驗次數和鍵值預算的動態信號。
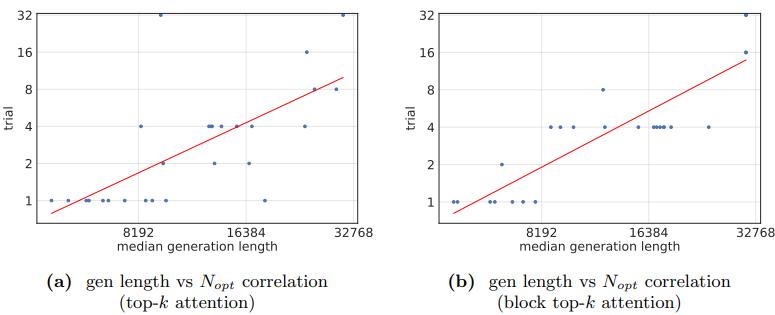
(來源:arXiv)
此外,稀疏的注意力大大降低了推理成本,使得更多的推理試驗和更長的生成成爲可能,這爲在固定資源預算內配置測試時擴展策略提供了更大的靈活性。
同時,通過將關注點從 token 級指標轉向任務級吞吐量,研究團隊認爲本次成果能爲算法與系統的協同設計開闢更廣闊的空間。需要說明的是,本次研究本質上屬於算法層面的成果,並不針對特定應用。儘管大模型可能被惡意濫用,但本研究並未引入現有系統之外的新能力或風險。
研究團隊表示,測試時擴展可能會消耗大量能源,引發人們對廣泛部署的環境可持續性的擔憂。而通過推廣稀疏注意力,他們希望幫助減少推理系統的碳足跡和能耗,並助力實現更廣泛的可持續人工智能目標。
未來,他們希望這項研究能夠指導在模型架構、測試時策略和硬件系統方面的協同設計,以便更好地解鎖下一波大模型擴展的潛力。
參考資料:
https://arxiv.org/pdf/2506.05333





