此前,業界對AI 能力的評價往往基於“會不會做題”,比如能不能在高考試題上擊敗人類考生、在奧數競賽中斬獲幾塊金牌,又或者寫出的代碼夠不夠格通過互聯網大廠的筆試……
但在這些看似“人類一敗塗地,AI大獲全勝”的測試背後,科學界一直存在一種冷靜甚至審慎的看法:AI 確實很會“做題”,但它能解決那些人類尚未解決的“真問題”嗎?畢竟,背誦教科書是一回事,拓展人類知識的邊界則是完全不同的另一回事。
許多科學家曾認爲,目前的 AI 或許只能做簡單的模仿者,無法進行深度的邏輯推理和創新。然而,Google Research 最新發布的一項重磅研究打破了這種質疑,並向我們展示:AI 不僅是隻會做選擇題的學生,還可以成爲人類頂尖學者的“左膀右臂”,共同攻克多個困擾學界已久的難題。

(來源:arXiv)
2 月 3 日,Google Research 聯合卡內基梅隆大學、哈佛大學、麻省理工學院等多所頂尖高校研究人員共同在預印本平臺 arXiv 提交了一篇論文:《利用 Gemini 加速科學研究:案例研究與通用技術》(Accelerating Scientific Research with Gemini: Case Studies and Common Techniques),詳細記錄了前沿大語言模型,特別是具備增強推理能力的 Gemini Deep Think 及其變體,如何從傳統的輔助工具轉變爲理論科學研究中的實質性合作者。
研究團隊通過展示 Gemini 系列大型語言模型在理論計算機科學、物理學、經濟學等多個領域的實際應用,證實了 Gemini 在解決開放性數學問題、反駁長期存在的猜想以及生成複雜新證明方面具備卓越性能,還總結出了一套行之有效的人機協作方法論。
爲了讓 Gemini 真正參與專家級的科研工作,研究人員首先構建了幾項關鍵的協作規則。首先是“迭代提示與改進”,即模型很少能一次性解決深奧問題,需要通過多輪對話,由人類研究員將大問題分解爲可驗證的子任務,並提供高層級的證明框架(即“腳手架”),引導模型逐步填補技術細節。
其次是“思想的異花授粉”(Cross-Pollination of Ideas),團隊利用模型攝取了跨學科海量文獻的優勢,藉助其識別出不同數學領域之間,可能被人類專家忽視的隱祕聯繫。
此外還有“神經符號循環”(Neuro-Symbolic Loops)技術,即將模型嵌入自動化的編程環境中,讓模型生成數學公式,同時編寫代碼對假設進行數值驗證,根據執行錯誤(如 Python 回溯信息)自主修正推導路徑,從而在沒有人類干預的情況下修剪無效的推理分支,形成一個自我修正的閉環。
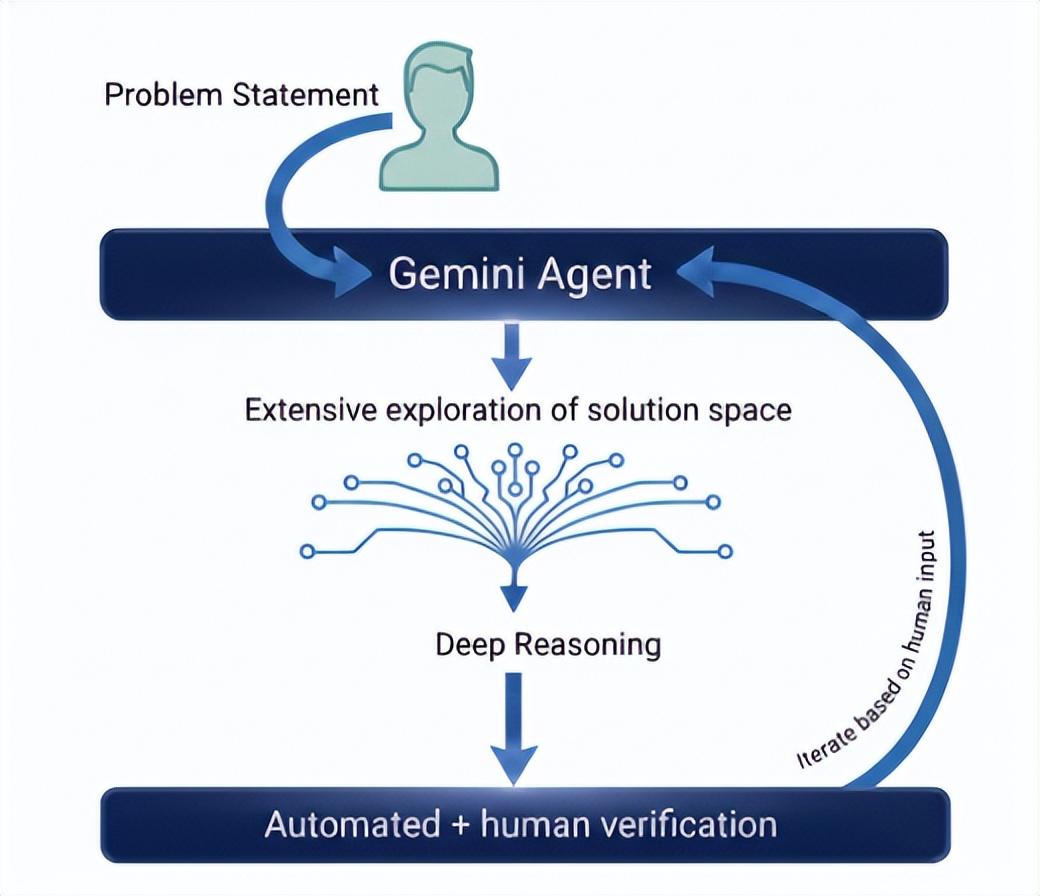
(來源:Google Research)
這些框架搭建完成後,Gemini 隨即在分屬多個領域的科學研究中展現出巨大的應用潛力。首先,在密碼學領域,Gemini 指出了一種前沿協議的致命漏洞。這一名爲“簡潔非交互式論證”(SNARGs)的協議,旨在保護區塊鏈和隱私計算,如果這個錯誤未被發現,未來的數字安全可能面臨巨大風險。
具體來看,針對一篇聲稱基於容錯學習(LWE)假設實現簡潔非交互式論證(SNARGs)的預印本論文,研究人員設計了一種“對抗性自我糾正”的提示策略,要求模型嚴格批判自己的發現。結果,Gemini 敏銳地指出,論文中“完美一致性”定義與實際構造僅能實現“統計一致性”之間存在嚴重的邏輯缺陷,這一發現隨後得到了密碼學專家和論文原作者的確認。
“在線次模福利最大化”(online submodular welfare maximization)是一個經典的經濟學與算法問題,研究如何在需求未知且逐個出現的情況下,例如在實時廣告競價或雲計算資源分配中,將資源分給不同的人以最大化整體滿意度。這裏的“次模”指的是邊際效益遞減,即擁有的越多,新獲得的價值就越低。
此前,谷歌研究科學家尼蒂什·科魯拉(Nitish Korula)等人提出過一個與之相關的猜想,認爲某種貪婪算法的效率界限可以被進一步提升。基於此,Gemini 並未順着原假設的思路進一步證實,反而自主構建了一個涉及 3 個物品和 2 個代理的具體反例,並通過繁瑣的期望計算成功反駁了該猜想。這是 AI 罕見地在研究者沒有給出明確答案的情況下,直接利用真實科研語境否定了一位人類學者(還是谷歌自己人)提出的猜想。

(來源:Recherche-Research-Google)
藉助掌握海量跨學科知識的優勢,Gemini 在數學領域的難題中另闢蹊徑,爲算法難題提供頗具創新性的幾何解法。最大割(Max-Cut)是一個圖論問題,旨在尋找一種分割方式,使被切斷的連接線數量最大,這也是網絡流和芯片設計中常用的基礎算法之一。
爲解決其中關於近似算法精度的一個長期開放問題,Gemini 跳出了傳統的組合優化思路,將其重構爲一個幾何泛函分析問題,並創造性地建議應用斯通-魏爾斯特拉斯(Stone-Weierstrass)定理(一項關於函數逼近的數學定理)來建立必要的方差界限。
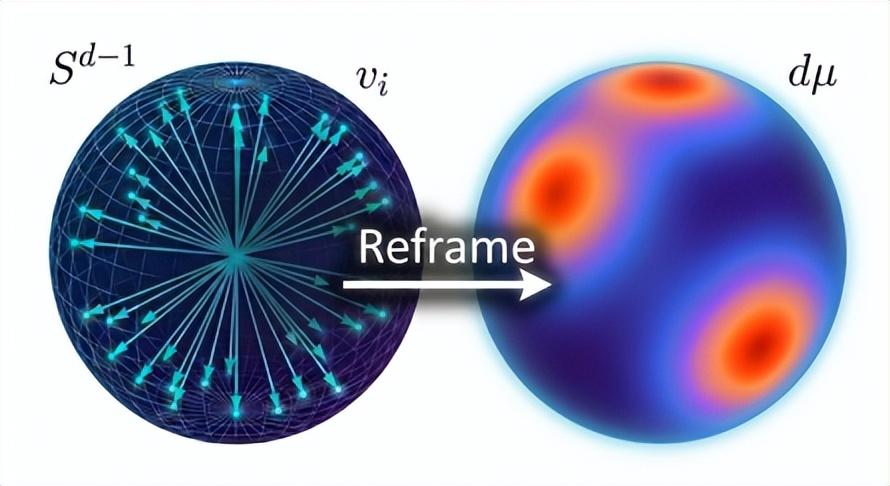
(來源:Google Research)
在計算幾何領域中,針對斯坦納樹問題(如何以最短路徑連接多個點),存在一個關於“單純形是最佳圖嵌入結構”的猜想。Gemini 發現,解決問題的關鍵實際在於希爾伯特空間映射中的基爾斯布勞恩(Kirszbraun)擴展定理,這個定理通常用於分析函數的平滑性(Lipschitz 連續性),人類研究者此前往往認爲它過於深奧而不予考慮。但 Gemini 正是藉助這一晦澀的數學工具,成功完成了從任意圖嵌入到星形圖嵌入的形式化映射證明。
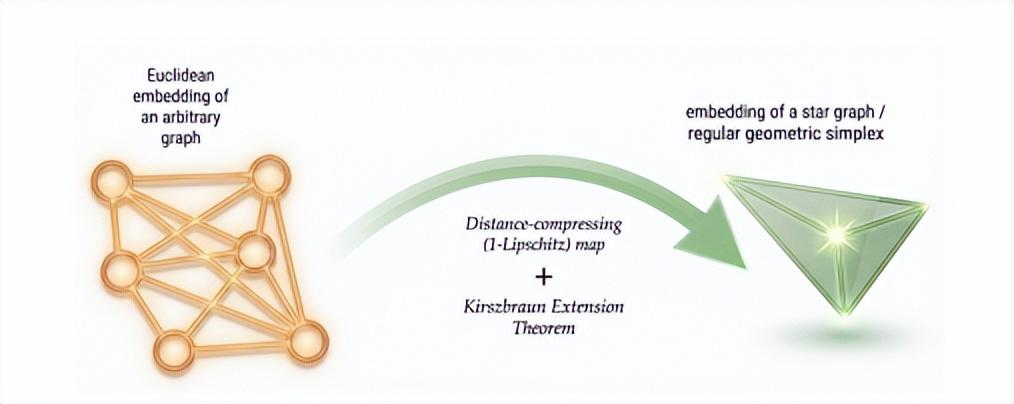
(來源:Google Research)
類似地,正則二分圖常用於通信網絡建模,爲改進其完美匹配數量下界,Gemini 綜合運用了統計物理中的貝特(Bethe)近似、數論中的互質整數分析以及譜圖理論中的伊原-巴斯(Ihara-Bass)恆等式,給出了比施賴弗(Schrijver)界限更強的理論結果。
涉及複雜運算和算法優化的學科時,Gemini 展現出驚人的“精算師”與“優化師”能力。在理論天體物理學中,科學家試圖通過引力波探測宇宙大爆炸後的遺蹟——宇宙弦。然而,預測其引力輻射涉及一個極度振盪且具有嚴重奇點的球面積分計算,這是該領域的一個長期難題。
爲此,研究團隊構建了一個神經符號系統,Gemini 在其中推導數學公式,並編寫 Python 代碼與數值基準進行比對。通過這種反饋循環,AI 自主發現了六種不同的解析路徑,最終結合蓋根鮑爾(Gegenbauer)多項式展開,爲這一難題推導出一個精確的閉式解。
在大數據處理中,如何在有限的內存中從海量數據流裏篩選出最有價值的信息(次模函數最大化)是一個核心問題,Gemini 敏銳地發現,現有分析中存在一個潛在自由度:算法中的閾值參數不應是全局固定的,而應根據處理狀態動態調整。
通過引入狀態依賴閾值,AI 推導並證明出一個優化的遞推關係,將算法的近似比從約 0.55 精確提升到了 2-√2。同時,在流算法的香農熵(Shannon Entropy)估計中,AI 觀察到,算法其實只需依賴低階矩,從而避開了高方差區域,這一洞察直接將內部狀態變化的複雜度界限從多項式級大幅優化至多對數級別。
此外,論文還證實,Gemini 已經有能力重塑論文寫作的全流程,甚至出現了“代碼化”論文寫作的趨勢。例如,在理論計算機科學領域,著名的複雜性理論專家、Computational Complexity 博客博主蘭斯·福特諾(Lance Fortnow)嘗試使用集成了 AI 的 IDE 開發環境,通過高層級的提示進行“氛圍編程”(Vibe-coding)。
當對複雜性類 SP2(涉及博弈論與計算複雜性)進行研究時,Gemini 不僅可在幾乎沒有人工干預的情況下,自主生成關於搜索問題與決策問題等價性的主要證明,被指出推論中的假設錯誤後,還迅速將證明策略修正爲歸約法,幾乎獨立完成了一篇高質量理論論文的初稿。
論文還在更多學科中考驗了 Gemini 解決實際難題的能力。如在機制設計領域,AI 幫助將原論文中基於有理數報價的結論推廣到了實數域,利用拓撲學和序理論替代了原有的計數性論證。
在信息論領域,AI 通過分析優化圖景和利用超壓縮性不等式(Hypercontractivity),對著名的庫爾塔德-庫馬爾(Courtade-Kumar)猜想做出了實質性貢獻,包括將其推廣到非平衡函數以及改進了高噪聲區間的界限。
這一系列成果表明,前沿 AI 模型已經具備了在理論科學中進行實質性貢獻的能力,而非簡單的輔助工具。它不僅能優化算法、推導公式,還能跨越學科壁壘,甚至從人類專家的盲點區域找到新的可能性。
然而,論文也強調,目前的這種成功仍高度依賴於人類專家的“腳手架”支持和嚴格驗證,類似於目前已廣爲人知的“Vibe-coding”,這種人機協作模式被形象地稱爲“Vibe-proving”——即利用 AI 的直覺生成證明草稿,再由人類進行嚴格審查。
爲了徹底解決模型可能產生的幻覺問題,未來的研究方向將是用利用 Lean 或 Coq 等交互式定理證明器,將 AI 生成的非形式化數學推導轉化爲絕對嚴謹的形式化證明,從而在根本上保證科學發現的正確性,甚至有望得到同行評審的信任。
參考資料:
https://arxiv.org/pdf/2602.03837
排版:劉雅坤





